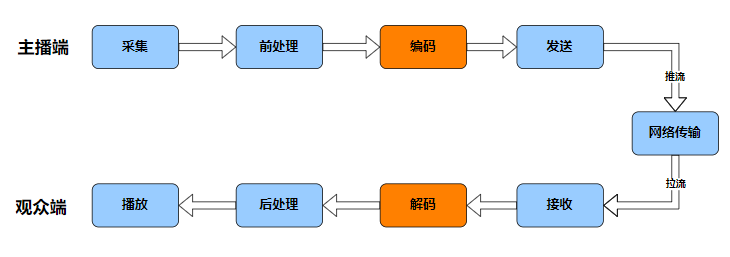
在音频编解码中,MDCT变换是一个非常重要的基础概念,它在MP3和OGG介绍中都有涉及到。MDCT变换是一种数学变换,它将时域信号转换为频域信号,这对于音频编解码来说非常关键。很多编码算法都会用到MDCT变换,因此深入了解它的原理和相关代码是非常有必要的。本文将着重介绍MDCT变换的原理和实现方法,希望能够帮助读者更好地理解音频编解码的基础知识,从而提高编码的效率和质量。如果您对音频编解码感兴趣,或者正在学习相关知识,那么本文将是一个不错的参考资料。
MDCT介绍
在处理语音和音频时,我们经常需要将信号分割成段或窗口,因为
- 音频信号随时间变化相对缓慢,因此通过在短窗口内分割信号可以假设信号是静止的,这是许多有效方法(例如频谱分析)的先决条件,
- 变换域分析(例如频谱分析)要求我们在一次操作中变换整个信号,这反过来又要求我们在开始处理之前接收到整个信号。例如,在电信中,这意味着我们必须等待句子完成才能开始发送,因此在接收器处重建句子必须等到整个句子完成,从而导致通信显着延迟。
因此,在实际场景中,我们总是在处理之前应用加窗。
离散傅里叶变换 (DFT) 和离散余弦变换 (DCT) 执行类似的功能:它们都将有限长度离散时间向量分解为缩放和移位基函数的总和。两者之间的区别在于每个变换所使用的基函数的类型;DFT 使用一组调和相关的复指数函数,而 DCT 仅使用(实值)余弦函数。
- DFT 广泛用于通用光谱分析应用,并已进入多个领域。它还用作利用信号频域表示属性的技术的构建块,例如重叠保存和重叠相加快速卷积算法。
- DCT 经常用于有损数据压缩应用,例如 JPEG 图像格式。DCT 非常适合压缩的特性是其高度的“频谱压缩”;在定性层面上,与 DFT 等其他变换相比,信号的 DCT 表示往往会将更多能量集中在少量系数中。这对于压缩算法来说是理想的;如果您可以使用相对较小的 DCT 系数集来近似表示原始(时域或空间域)信号,那么您可以通过仅存储包含大量能量的 DCT 输出来减少数据存储要求。
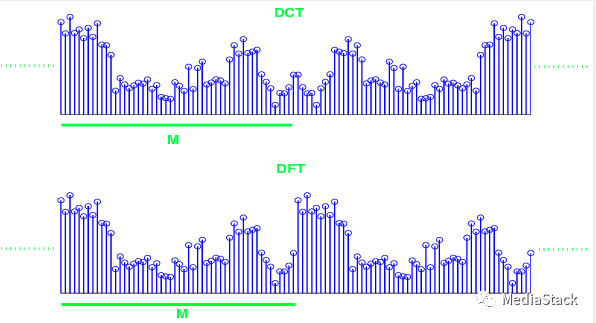
比较DFT和DCT的三角基的能量压缩能力和傅里叶谱分析的分辨率。变换能量压缩能力是指变换将信号能量重新分配为少量变换系数的能力。它可以通过携带一定(相当大)百分比的信号能量的信号变换系数总数的分数来表征。对于给定的能量百分比,该分数越低,变换能量压缩能力就越好。这一特性在大多数应用中是决定性的。
信号频谱估计中的变换分辨能力表征了在这些基底中测量的正弦信号的频谱峰值的锐度。它可以用数字方式评估为频谱峰值的宽度(以离散化间隔的分数表示),其中包含正弦信号能量的给定(实质性)百分比。根据采样理论,信号离散频谱中的频谱峰值的宽度通常与频域中的离散化间隔成正比。然而,对于上述三角变换所采用的傅里叶积分的不同离散表示,比例系数是不同的。
变换能量压缩能力的纯分析评估也是有问题的,因为它仅对于非常有限的信号数学模型是可行的。另一种选择是通过实验评估一些“典型”测试信号。我们展示了对一组 MPEG 音频测试信号以及一些经典和流行音乐信号的评估结果。对于这些信号,比较了具有和不具有窗函数的不同窗口大小(256、512 和 1024 个样本)的变换的能量压缩能力,以及对数十万个样本的大信号序列的平均值。结果下图所示,以信号频率带宽归一化的频率坐标表示。
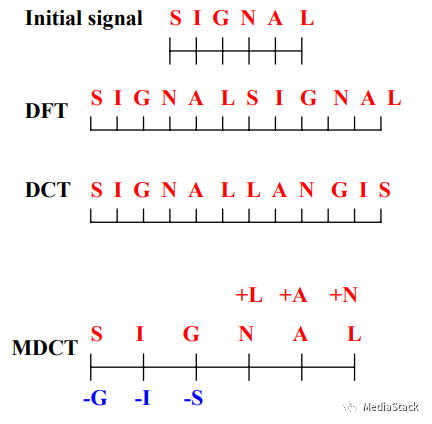
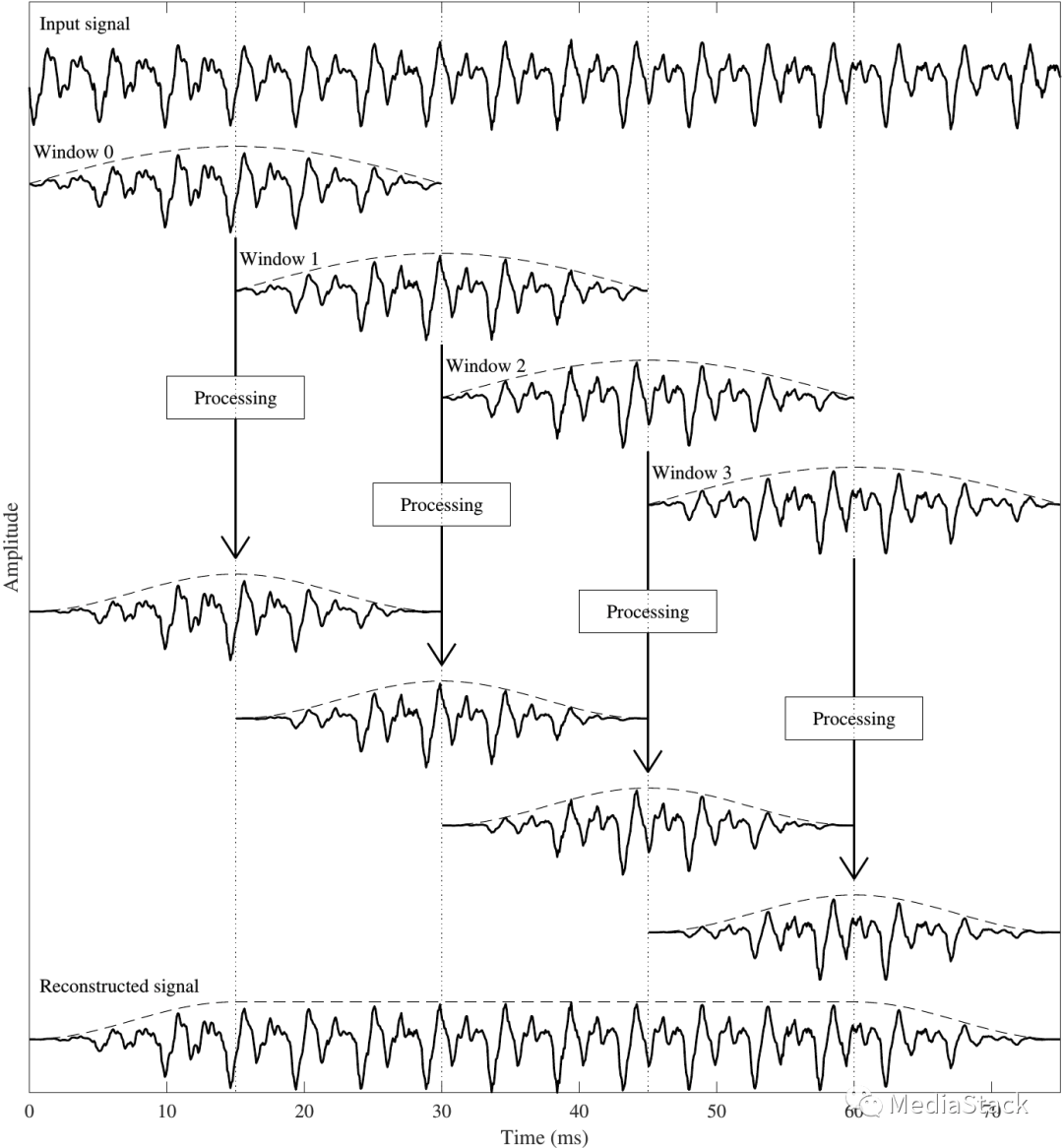
然而,在信号中应用光谱处理(例如STFT域中的处理)具有显着的缺点。我们需要重叠的窗口以允许完美重建,也就是说,要求我们能够从加窗信号完美地重建原始信号。然而,重叠意味着连续的窗口共享来自相同样本的信息(参见右图)。因此必须在两个窗口中对相同的信息进行编码,这是非常低效的。通过对信号进行编码,主要目的是为了将信息压缩到尽可能少的比特位,但如果对部分信息进行两次编码,就会增加需要编码的信息量。因此,STFT 域会导致过渡编码,实际上,两个不同的比特流可以代表相同的输出信号。
改进的离散预算变换(MDCT)是过度编码问题的解决方案,它在重叠处使用投影算子,使得连续窗口中的信息彼此正交。由于信息因此被完美保留,信息量没有增加也没有减少,我们说这个算子是临界采样。
因此,MDCT 提供了输入信号的时频表示,可以在其中分析和处理频率分量的时间演化。它具有 STFT 的大部分有益特性,其中在 MDCT 域中处理的信号在时域中保持连续,并且我们可以使用基于 FFT 的运算来高效实现。除了 MDCT 的完美采样之外,也许 STFT 和 MDCT 之间最显着的区别在于,当 STFT 是复值表示时,MDCT 在输入为实值时是实值表示。
由于 MDCT 的这些有益特性,它成为语音和音频编码中最常用的时频变换,并用于 MPEG USAC、3GPP EVS 和蓝牙 LC3 等标准化编解码器中。
MDCT算法简介
MDCT 基于在重叠处获取信号的对称和反对称部分,使得对称部分进入一个窗口而反对称部分进入另一个窗口。我们进一步对那些对称和反对称部分进行加窗,以便它们在边界处平滑地收敛到零。因此,连续窗口在重叠处是正交的,这样信息就被精确地分成两半,我们获得了完美的重建和临界采样。此外,由于这些段是窗口化的,因此我们不会遇到任何不连续性的困难。
其次,对加窗信号(正交投影)进行离散余弦变换(DCT)。然而,传统的 DCT 必须进行调整,使其相位和对称性与对称和反对称部分相匹配。因此,修改后的DCT和MDCT。对称性匹配只能通过 DCT 的这种修改来实现,并且不能推广到离散傅立叶变换 (DFT)。
信号的(反对)对称部分“看起来就像具有这种对称性的信号”。换句话说,我们引入了与原始信号的偏差,这种偏差被称为时域混叠分量,因为它类似于 DFT 中出现的混叠效应。然而,在重建过程中,我们将对称部分和反对称部分加在一起,使它们相互抵消,这称为时域混叠消除(TDAC)。TDAC相当于MDCT基础上的正交投影,因此是MDCT的核心属性。
MDCT函数变换
MDCT的函数公式可以参考如下链接,数学公式推导不是自己的强项,有兴趣的可以参考如下链接:
https://blog.csdn.net/wsygyb/article/details/104321778
https://wiki.aalto.fi/pages/viewpage.action?pageId=151499796
FFMPEG实现
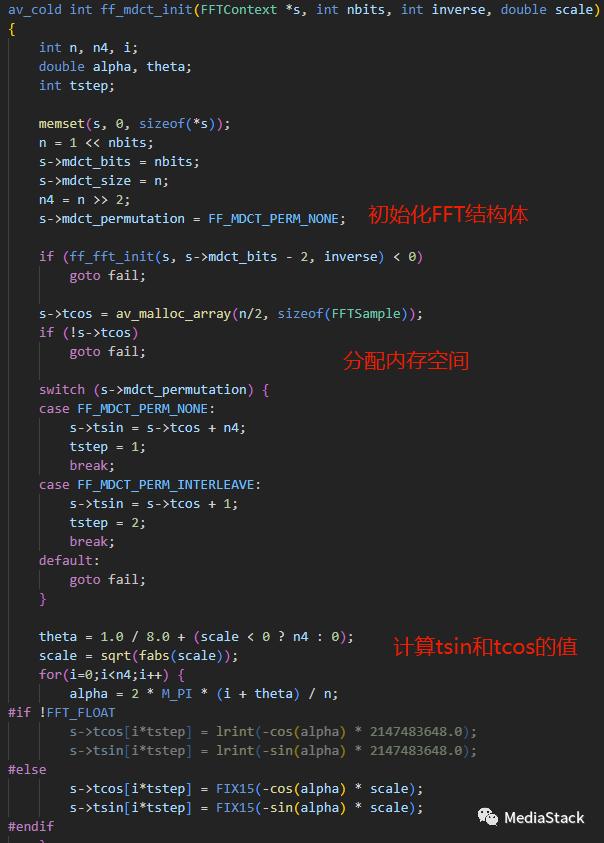
ff_mdct_init()
该函数用于初始化MDCT或IMDCT计算。
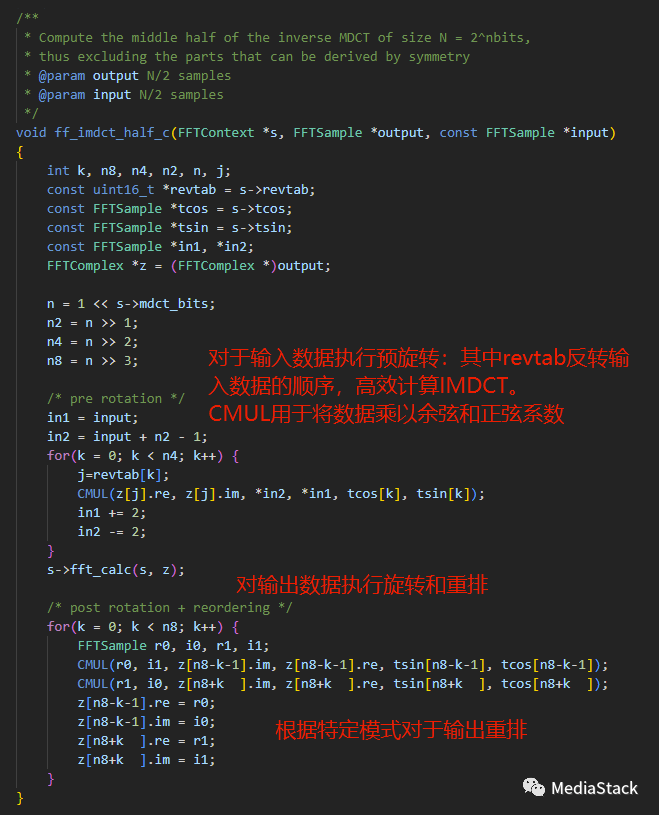
ff_imdct_half_c()
该函数计算大小为 N = 2^nbits 的逆 MDCT 的中半部分,从而排除可以通过对称性导出的部分。
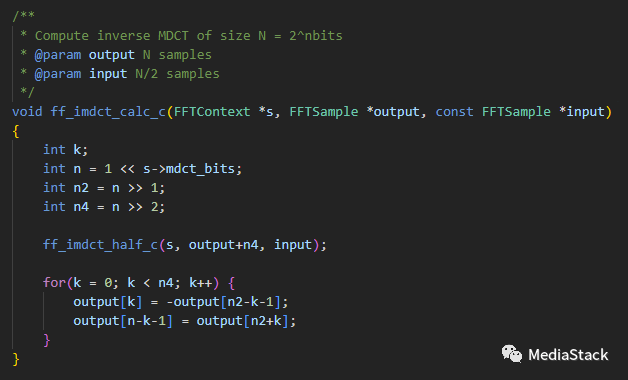
ff_imdct_calc_c()
该函数用于计算逆MDCT。
ff_mdct_calc_c()
该函数计算大小为 N = 2^nbits 的 MDCT
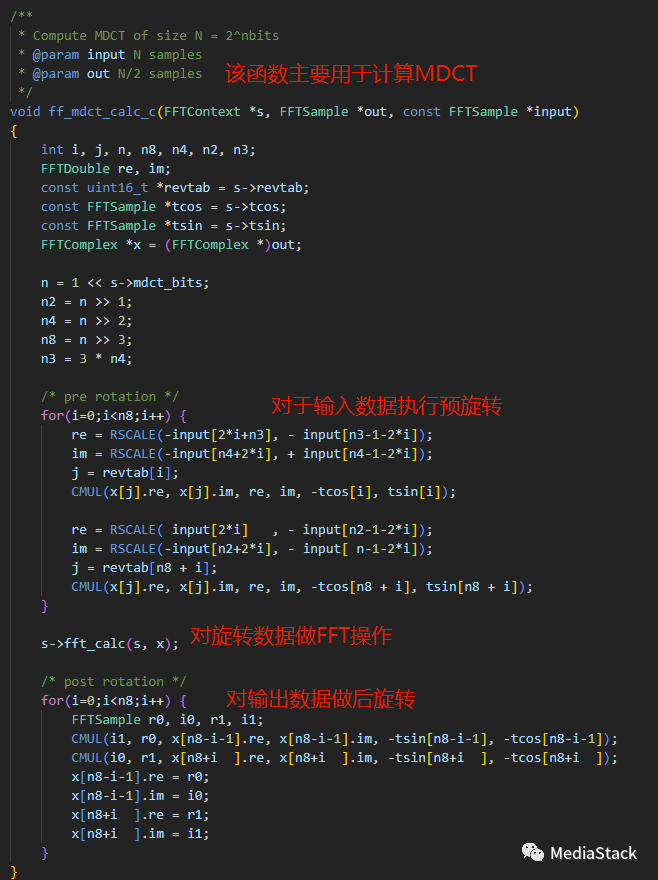
至此,libavcodec\mdct_template.c分析完成。有兴趣的可以结合实际使用场景更深入的学习。
作者信息:我是一枚爱跑步的程序猿,维护公众号和知乎专栏《MediaStack》,有兴趣可以关注,一起学习音视频知识,时不时分享实战经验。
原文:https://mp.weixin.qq.com/s/Qms97amBD7FAD5T4yU4T6Q
版权声明:本文内容转自互联网,本文观点仅代表作者本人。本站仅提供信息存储空间服务,所有权归原作者所有。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至1393616908@qq.com 举报,一经查实,本站将立刻删除。